数学が苦手なあなたへ 数学ができるようになるためのステップを解説
2020年05月14日

こんにちは。生徒さんの勉強とメンタルを完全個別指導でサポートする完全個別指導塾・キズキ共育塾です。
あなたは、「数学ができない…」とお悩みではありませんか?
- がんばって公式を覚えたけど、どう使ったらいいかわからない。
- 学校のテストはできるのに、模試や入試問題だと理解できない。
そんな人は、あなた以外にもたくさんいます。
このコラムでは、数学ができないと悩む人に向けて、数学ができない人の4つの特徴と、数学ができるようになるための6つのステップについて解説します。
具体的に言うと、数学ができるようになるには、定義を大切にすることや、考えながら答えを見るといったことが大切です。
では、詳しく見ていきましょう。
私たちキズキ共育塾は、数学ができない人のための、完全1対1の個別指導塾です。
生徒さんひとりひとりに合わせた学習面・生活面・メンタル面のサポートを行なっています。進路/勉強/受験/生活などについての無料相談もできますので、お気軽にご連絡ください。
数学ができない人の4つの特徴
この章では、数学ができない人の特徴について解説します。
自分に当てはまるようでも落ち込まず、後で紹介する6つのステップを行うことで、数学ができるようになっていきますよ。
特徴①数学が暗記科目になっている

数学の勉強を、「公式を覚える!」「解答を丸暗記する!」というふうに行っていませんか?
数学を暗記で勉強している人は、一度やったことのある問題や似たような問題しか解くことができません。
数学ができるようになるには、覚えた公式を、いつ、どのように使うかを判断する力を養う必要があります。
特徴②基礎が身についていない
数学ができない人には、数学の基礎が定着していない傾向があります。
高校生なら中学の数学を、中学生なら小学校の算数を、きちんと理解していますか?
数学は積み重ねが大事な科目です。
また、数学の授業は、それまでに学んだ内容が身についている前提で進められます。
したがって、これまでの範囲でわからない部分があると、できない部分が増えていったり、授業に全くついていけなくなったりするのです。
特徴③すぐに答えを見る

数学ができない人の多くは、数学に対して強い苦手意識を持っています。
そして、問題を見てわからなければ、すぐにあきらめて答えを見てしまいます。
実際にこういった特徴のある生徒に話を聞いたところ、「答えがすぐに出ないものを考えるのは苦手だし、イライラする」と言っていました。
しかし、実は数学を勉強する目的のひとつが、わからない問題をどう解決するかを考える力を養うことなのです。
わからない問題の答えを見ること自体はダメではありませんが、答えを見る前にたくさん考えることが必要です。
特徴④予習・復習をしない
数学ができない人の多くは、ただ授業を受けるだけで、予習や復習をしない傾向にあります。
数学に限らず、勉強の内容は、一度学んだ(見た、聞いた、解いた)だけでは理解しづらいのです。
そのため、授業をスムーズに理解できるように予習をしたり、より定着するように復習をしたりという作業が、とても大切です。
数学を勉強することで身につく4つの数学的思考力
そもそも、なぜ数学を勉強するのでしょうか。
結論から言えば、数学は、数学的思考力を養うために勉強します。
この数学的思考力こそが、特徴③でも紹介したわからない問題をどう解決するかを考える力です。
数学的思考力を身につけることで、直接的に数学ができるようになるとともに、数学以外の場面でも生活が向上します。
この章では、数学を勉強することで身につく数学的思考力について解説します。
数学的思考力①情報を適切に分解して整理する力

情報を適切に分解して整理する力とは、問題の中から必要な情報を箇条書きや表にして整理する力のことです。
直接数学に関係する部分では、問題文をいくつかの条件に分割したり、どの条件が大切かを判断したりするときに必要となります。
数学に関係ない部分では、情報の取捨選択が得意になるため、わかりやすく話すことができるようになります。
数学的思考力②モデル化(抽象化)する力
モデル化(抽象化)する力とは、不要な情報をそぎ落とし、本質のみを抜き出すことで、問題を単純化する力です。
数学に関係することでは、以下のようなことを行う力です。
- 文章題を解くときに、問題文の情報から式をつくる
- 偶数のことを、数字と記号を用いて2n(nは整数)と表す
ちょっと難しい話かもしれませんが、数学以外の例では、地図をつくるときには3次元的な情報から必要なものだけ取り出して、2次元的な情報に落とし込むことが行われています。
つまり、地図が存在するのはモデル化力を活かしている人たちのおかげと言えます。
また、モデル化されたものは物事の本質のみを表します。そのため、どうすれば問題を解決できるかという問題解決のプロセスが見えやすくなります。
数学的思考力③具体化する力

具体化する力とは、具体的に試してみて、物事を把握する力のことです。
数学の問題を解いているときに、文字が多くてわかりづらいと思ったことがありませんか?
そのとき、具体的な数字を当てはめてみると、問題がどのようなことを言っているかを把握しやすいです。
数学に直接関係する例は、以下のような問題を解くときです。
【例題】
長さ1cmにつき重さ10gのハリガネがある。このハリガネx cmのときの重さを y gとする。yをxの式で表せ。
この問題に、具体的な数字として、1cm、2cm、3cmを当てはめて考えてみると、以下ののようになります。
- 1 cmだと……10 g
- 2 cmだと……20 g
- 3 cmだと……30 g
すると、ハリガネの長さを10倍すれば重さが出るということがわかります。
よって答えは、y = 10 x であるとわかります。
このように、具体化することで問題がとらえやすくなり、式を簡単につくることができました。
数学以外の場面では、何か問題が起きたときに、対応法を具体的に考えることが可能になり、対処しやすくなります。
数学的思考力④表現する力
表現する力は、言葉どおり、自分の考えなどを表現して他人に伝える力のことです。
論理的に考える力とも密接にかかわっています。
数学においては、定理の証明や文章形式の解答をつくるときに必要な力です。
数学以外では、例えば日常生活の中で、思っていることを人に伝えるときに役立ちます。
部活や仕事の場面でも、新しいアイディアや問題解決のプロセスを思いついたとき、それを上手に伝えるために大いに役立つ力です。
数学的思考力を伝えることで、数学以外の解決能力も上がります
紹介した4つの数学的思考力を一度に鍛えることができる科目が数学です。
すなわち、数学をしっかりと学べば、社会に出てから直面する困難や問題を解決する能力が格段に上がるということです。
「今でしょ」で有名な林修先生も、あるテレビ番組で、「数学的思考力を養うことができるからこそ、学校で勉強する科目の中では数学が一番大切である」とおっしゃっていました。
これからは、数学的思考力を身につけることを目標に、数学を勉強しましょう。
数学ができるようになるための6つのステップ
この章では、数学ができるようになるための6つのステップについて解説します。
ステップ①まずは自分の実力を知ろう

まず、自分の学力を把握しましょう。
先ほども言ったとおり、数学は積み重ねが大事です。
自分が理解している範囲を把握し、わからない部分を基礎からしっかり積み重ねていくことで、数学ができるようになっていきます。
実力を知るためには、学校の定期テストや模試の結果を活用するのがオススメです。
試験の結果を見ることで、ここまではできている、中学レベルが定着していない、この分野が苦手というような分析ができます。
ただし、数学が苦手な人が、自分だけで自分の実力を分析することは難しいでしょう。
恥ずかしがらずに、学校や塾の先生に自分の実力がどのくらいなのか知りたいと相談してみましょう。
なお、自分の実力がわかっている場合も、実力の範囲内(わかっている範囲内)の問題だけを繰り返し解いているようなら、数学はできるようになりませんので注意してください。
ステップ②定義を大切にしよう
いざ数学の勉強(学び直し)を始めたら、最も大切にしてほしいのは、数学で出てくるいろんな言葉の定義を覚えると言うことです。
定義とは、その言葉の説明やあらかじめ決められた共通の認識と言い換えることができます。
なぜ定義が大切かと言うと、それが数学の土台だからです。
いろんな言葉の定義をしっかり理解することで、問題の意味や解き方もわかってきます。
例:平行四辺形
平行四辺形という言葉の定義を理解していないと、平行四辺形に関係する問題は意味が全くわからない状態となります。
平行四辺形の定義は、二組の対辺がそれぞれ平行な四角形です。
そして、平行四辺形の定義は、二組の対辺がそれぞれ平行な四角形というただ1つだけです。
平行四辺形の特徴として有名な向かい合う辺の長さが等しいや、向かい合う角の大きさが等しいなどは、定義ではなく定理、性質、公式などと呼ばれます。
このように、定義を理解すると、定理や公式の意味も理解できるようになります。
実際に、平行四辺形の定理は、全て定義から導くことができます。
定理の一つ、平行四辺形は、向かい合う2組の辺が等しいことを、例題でご紹介します。
数学が苦手で以下の例題の意味を理解できない場合には、今は例題の内容は無視して構いません。
定義から定理を導ける=定義を覚えると数学ができるようになる、ということだけ覚えておいてください。
【例題】
平行四辺形の、向かいあう2組の辺が等しいことを証明せよ。証明したいこと:AB=CD 、 AD=CB
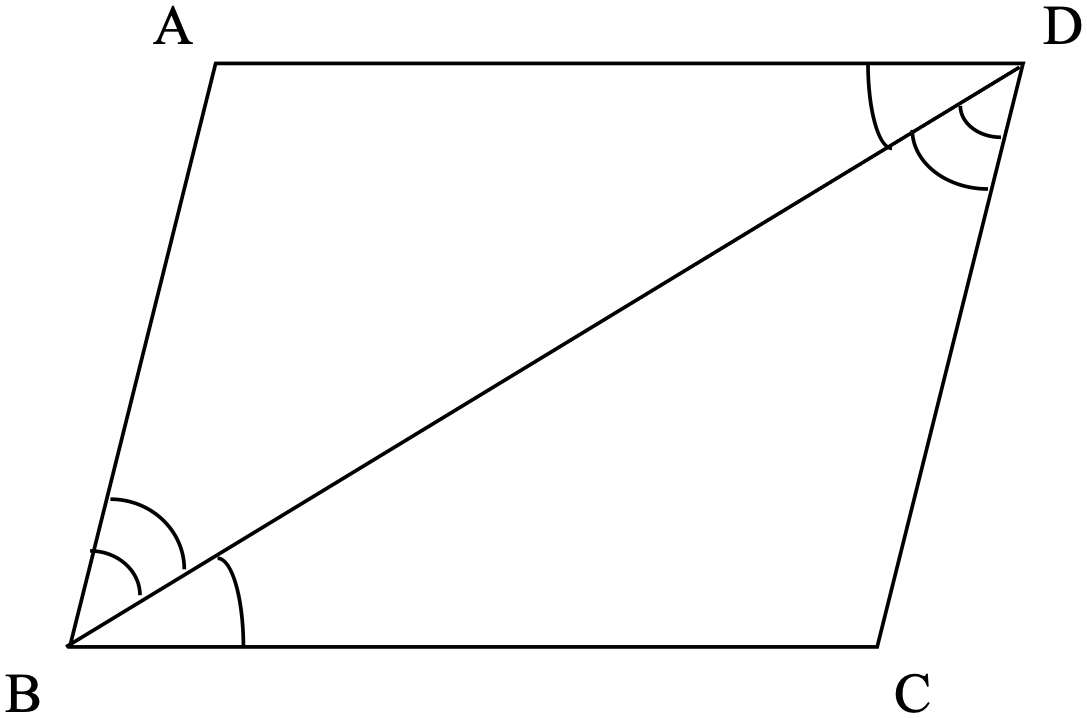
【証明】
平行四辺形ABCDに対角線BDを取る。
平行四辺形の定義から、ABとCDは平行。
平行線の錯角は等しいので、
∠ABD=∠CDB
∠ADB=∠CBD
また、辺BDは共通。
よって、一辺とその両端の角が等しいので、
三角形ABDと三角形ABCは合同。
したがって、AB=CD 、AD=CB
ステップ③公式が導かれる過程を知ろう
定義を覚えたら、さきほどの例題の平行四辺形の向かい合う2組の辺が等しいことの証明のような、定義から性質・定理・公式が導かれる過程を学びましょう。
公式が導かれる過程を知ることで、公式の本質や意味が理解でき、数学が上達していきます。
できそうであれば、以下のようなことをやってみてください。もちろん、今苦手な場合は、学校や塾の先生を頼って大丈夫です。
- 二等辺三角形の定義、二辺が等しいから、性質、底角が等しいことを導く
- 三角比の定義から、三角比の相互関係の式を導く
- 2点間の距離の公式を使って、円を表す方程式をつくる
意味を理解していると覚えやすいものは、数学以外でもたくさんあります。
例えば、料理をするときの具材を調理する順番です。
煮物の場合、以下のようなルールが理解できると思います。
- 火のとおりにくい具材は、早いうちに炒め始める
- 煮崩れしやすい具材は、最後の方に入れる
このように、調理の順番をなぜそうするのかをセットで覚えておきましょう。そうすれば、単純に暗記するよりも忘れにくくなりますよね。
数学も同じで、公式がそうなっている理由を理解していると、問題を解く力がグッと上がるのです。
数学の公式を覚えるときも、ただ暗記するのではなく、どういう意味なのか、どう導かれたのかを一緒に覚えておくようにしましょう。
ステップ④練習問題をたくさん解こう
次は、例題や基礎的な練習問題をたくさん解きましょう。
たくさん解けば解くほど、数学はできるようになります。
オススメの教材は、教科書・問題集・市販の参考書の、例題・練習問題です。
ただ、世間には参考書や問題集がたくさんあるので、どれを選べばいいのかわからないかもしれませんね。
数学ができない中高生が数学をできるようになるためには、チャート式がオススメです。
その理由は、以下の2つです。
- 白チャートや青チャートなど、色でレベル分けがされていて、自分に合ったものを選べる
- 例題と練習問題が同じページに載っているので、例題で学んだことをすぐに実践できる
もし、このステップ④で難しいと感じる場合は、公式の理解ができていないか、これまで勉強したはずの単元の内容が定着していない可能性が高いです。
ステップ③までのどこでつまづいているのかを、先生など頼りながら、もう一度確認しましょう。
ステップ⑤応用問題を解いてみよう

基礎的な問題が解けるようになったら、応用問題を解いてみましょう。
例えば、以下のようなものです。
- 問題集で応用例題や発展となっている問題
- 参考書で重要例題や入試レベルと書いてある問題
- 実際の入試の過去問(問題の最後に高校や大学の名前が書いてあるもの)
以上の問題は、公式を工夫して使わなければいけなかったり、以前に学んだ内容と組み合わせて解く必要があったりします。
一筋縄ではいかないはずですが、挑戦してみてください。
ここでわからないからとすぐにあきらめると、数学はできるようになりません。
考えれば考えただけ、数学的思考力を上げることにつながります。わからない場合でも、1問につき最低でも5分以上は考えるのがよいと思います。
ステップ⑥答えを見よう
一つの問題を5分以上考えてもわからないときは、思い切って答えを見てしまいましょう。
ただし、以下のことを考えながら答えを見るようにしましょう。
- 問題文の中で大事な情報は何だったか
- 使われている公式がなぜ必要だったのか
- 自分に足りない知識は何だったのか
この3つを考えながら答えを見ることで、覚えた公式をいつ、どのように使うかを判断する力を鍛えることができます。
この力がついてくれば、応用問題であっても簡単に解けるようになるはずです。
問題の解き方・考え方の例題
最後に、どのように数学の問題を解くのか、何を考えながら答えを見るのかを示す例題を載せておきます。
なお、この問題も、今数学が苦手なら理解できないかもしれません(また、高校生向けですので、中学生の方は理解できないと思います)。
今理解できなくても「自分は数学ができない…」と落ち込む必要はありません。これまでご紹介したステップを一歩ずつ進むことで、理解できるようになります。
【問題】
0°≦θ≦180°であるとき、y=cos2θ+sinθ+1 とする。
yの最大値とそのときのθの値を求めよ。
解答は、わからなくても5分くらい考えましょう。
その後に、こちらの画像(解答)をご覧ください。
赤い文字は、公式や教科書の例題となっている基礎レベルの内容です。
青い文字は、実際の解答には不要ですが、問題を解くときや答えを見るときに考えてほしいポイントを表しています。
数学ができるようになるために、本当に必要なことは青文字の方になります。
このことを踏まえて、解答例をご覧ください。
まとめ~数学ができない状態は克服できます~

今回は、数学ができない人の4つの特徴と、数学ができるようになるための6つのステップを紹介しました。
大事なことは、以下の2つです。
この2つができれば、必ず数学はできるようになります。
そして、もし、やっぱりひとりで勉強するのは難しい、数学を、基礎からしっかり学び直したい、自分の実力がわからない、などと思うようでしたら、私たちキズキ共育塾にご連絡ください。ご相談は無料です。
完全個別指導の授業で、全力サポートします。
Q&A
よくある質問
数学ができない人の特徴を教えてください。
以下が考えられます。
- 数学が暗記科目になっている
- 基礎が身についていない
- すぐに答えを見る
- 予習・復習をしない
詳細については、こちらで解説しています。
数学ができるようになるためのステップを教えてください。
以下が考えられます。
- ステップ①まずは自分の実力を知ろう
- ステップ②定義を大切にしよう
- ステップ③公式が導かれる過程を知ろう
- ステップ④練習問題をたくさん解こう
- ステップ⑤応用問題を解いてみよう
- ステップ⑥答えを見よう
詳細については、こちらで解説しています。
監修 / キズキ代表 安田祐輔

やすだ・ゆうすけ。発達障害(ASD/ADHD)によるいじめ、転校、一家離散などを経て、不登校・偏差値30から学び直して20歳で国際基督教大学(ICU)入学。卒業後は新卒で総合商社へ入社するも、発達障害の特性も関連して、うつ病になり退職。その後、不登校などの方のための学習塾「キズキ共育塾」を設立。経歴や年齢を問わず、「もう一度勉強したい人」のために、完全個別指導を行う。また、不登校の子どものための家庭教師「キズキ家学」、発達障害やうつ病の方々のための就労移行支援事業所「キズキビジネスカレッジ」も運営。
【新著紹介】
『学校に居場所がないと感じる人のための 未来が変わる勉強法』
(2022年9月、KADOKAWA)
【略歴】
2011年 キズキ共育塾開塾(2025年6月現在17校+オンライン校)
2015年 株式会社キズキ設立
2019年 キズキビジネスカレッジ開校(2025年6月現在8校)
【メディア出演(一部)】
2022年 NHK総合「日曜討論」(テーマ:「子ども・若者の声 社会や政治にどう届ける?」/野田聖子こども政策担当大臣などとともに)
共同監修 / キズキ相談担当 半村進

はんむら・すすむ。1982年、茨城県生まれ。東京大学文学部卒。
小学校時代から転校を繰り返し、運動ができないこと、アトピー性皮膚炎、独特の体形などから、いじめの対象になったり、学校に行きづらくなっていたことも。大学に入学してようやく安心できるかと思ったが、病気やメンタルの不調もあり、5年半ほど引きこもり生活を送る。30歳で「初めてのアルバイト」としてキズキ共育塾の講師となり、英語・世界史・国語などを担当。現在はキズキの社員として、不登校・引きこもり・中退・発達障害・社会人などの学び直し・進路・生活改善などについて、総計1,000名以上からの相談を実施。
サイト運営 / キズキ
「もう一度学び直したい方」の勉強とメンタルを完全個別指導でサポートする学習塾。多様な生徒さんに対応(不登校・中退・引きこもりの当事者・経験者、通信制高校生・定時制高校生、勉強にブランクがある方、社会人、主婦・主夫、発達特性がある方など)。授業内容は、小学生レベルから難関大学受験レベルまで、希望や学力などに応じて柔軟に設定可能。トップページはこちら。2025年6月現在、全国に17校とオンライン校(全国対応)がある。